Computational materials design
Computational design is the linchpin within the Materials Design Engine here at the Leverhulme research centre where the transformative goal is prediction of experimentally realizable crystal structures and properties.
Current computational approaches have major limitations. Genetic algorithms, particle swarm optimisation, and Monte Carlo methods are heuristic and do not have an a priori guarantee of closeness to optimality. ‘Top down’ data-mining of known crystal structures does not produce new unit cells and asymmetric unit atom locations, and hence can only find close analogues. Conversely, ‘bottom up’ approaches to crystal structure prediction, including our own methods (Figure 1), become computationally intractable unless the system is highly constrained, both in terms of complexity and structural flexibility. Hence, computation today does not generally lower the barrier for us to design and discover new materials.
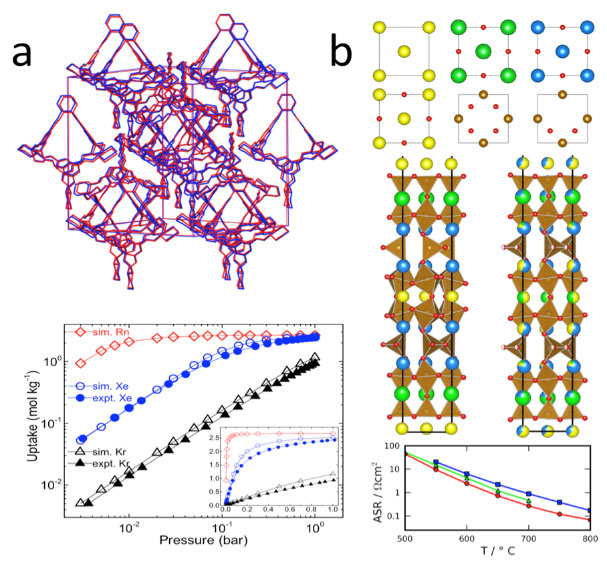
Figure 1: Tackling the design gap. We cannot design materials from the ‘atoms up’, but by defining larger ‘modules’, we have predicted structures and properties for (a) organic (Cooper et al., Nature, 2011) and (b) inorganic solids (Rosseinsky et al., Science, 2013).
Based only on knowledge of the chemical constituents across multiple materials types we will unlock the dream of truly ‘bottom up’ materials design giving rise to novel, complex systems which mimic biology. Building powerful new computer science solutions to this non-convex minimization problem, used here for the first time in a chemical context, will be emphasise this step change in materials design. The focus of this theme will be spread across key areas.
Exploring the Energy Landscape with the initial objective to translate the structure prediction problem from the language of Chemistry into Computer Science and then back to the experimental user base. This is not trivial, and requires extensive cross-disciplinary collaboration. Building on the standard hierarchy of energy computations of successively greater approximation, we will develop simplified energy functions capturing the essence of the global energy landscape in a form that readily translates the chemistry into Computer Science language (Ventre et al., SIAM J. Comput., 2014, 43, 1263).
Shared understanding from A will allow for the development of radical new optimisation solutions for the non-linear, non-convex structure prediction problem. Approximation algorithms can find solutions guaranteed to be ‘near’ the optimal solution for an NP-hard problem. For “worst case” NP-hard problems that cannot be approximated, we will strengthen existing heuristic methods by applying novel approaches. Artificial Intelligence will allow efficient exploration of the knowledge from our experimental programme and from the literature knowledge base to guide the approximation algorithms developed, by learning successful optimisation paths.
We will integrate these computational and searching processes into high-performance computing systems, using massive parallelism to implement computationally costly approaches. The combined product of B and C will be an open-source toolkit for materials engineers that forms a key sub-component in our Materials Design Engine.