July 2015 - Focus on Geometry in Liverpool

Image 1: (L-R) Oleg Karpenkov, Emily Howard and Anna Pratoussevitch
Since the beginning of my Leverhulme residency in Liverpool I’ve had a large number of individual meetings with DMS researchers. These meetings have been welcome opportunities for me to speak in depth with the researcher about an aspect of his or her research. I’ve been pleased to discover that the researchers tend to become highly energised, even passionate(!), when describing their own research and so far everyone has been highly skilled at explaining the (often complex) concepts they are dealing with in the simplest possible terms. I’m enjoying the challenge of trying to absorb so many new ideas and already I have a very long reading list.
Two such researchers are pure mathematicians Anna Pratoussevitch and Oleg Karpenkov, linked by their work in the field of geometry, a branch of mathematics that studies the shape, distance, length and area of spaces. The word geometry comes from the Ancient Greek and refers to the measurement of the Earth. Modern geometry has a vast range of applications, including Cartography and Navigation, Engineering and Physics, Design and Computer Graphics. In her research Anna focuses on questions about hyperbolic geometry. She explains: ‘Hyperbolic geometers study shapes of spaces with negative curvature. For example, curvature is negative for a surface at the points that look like a saddle point. In hyperbolic spaces we find very interesting phenomena that seem counter-intuitive from the point of view of the usual plane geometry: for example the sum of the angles of a triangle in the hyperbolic plane is less than 180 degrees.’
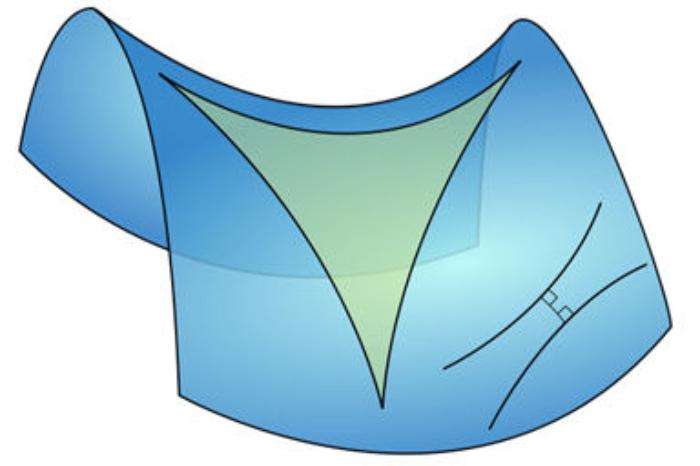
Image 2: Hyperbolic triangle immersed in a saddle-shape plane (Wikipedia Commons)
Oleg told me that his first experience of geometry goes back to number theory, another area of mathematics. It is difficult to separate geometry from other branches of mathematics and in Liverpool there are several groups dealing with different aspects of geometry such as Algebraic Geometry, Dynamical Systems and Geometry and Topology (the study of where and how objects develop irregularities). Anna and Oleg both belong to the Singularity Theory group alongside researchers Victor Goryunov, Peter Giblin and Jon Woolf. Oleg’s later research has shifted more towards areas of geometry that have applications in real life such as tensegrities (cable and rod structures). He says ‘I was attracted by the interplay of these research topics with real applications in art and modern architecture.’

Image 3: Needle Tower II by sculptor Kenneth Snelson (Wikipedia Commons)
Anna’s research also has links with visual art. When we first spoke, she handed me a paper about the polyhedron depicted in Albrecht Dürer’s engraving Melencolia I (1514) written by her late supervisor mathematician Egbert Brieskorn. Anna studies polyhedra directly related to Dürer’s solid, although many of them reside in higher dimensions (higher than 3D - it is hard to imagine how they could look!). I’m finding that these conversations about different geometries in different spaces are enabling me to think about my own music in new ways. I’ve recently begun work on a new orchestral piece titled ‘sphere’ and as I write, I’m imagining the act of composition as though it were the construction of a new geometry within a ‘sphere’.
Image 4: Durer’s solid fits into a series of polyhedra studied by Anna Pratoussevitch