Dissociation on Corrugated Surfaces

First a few words on what is meant by corrugated, and for that matter what it is that is corrugated.

Until recently, many people had thought that the interaction potentials for a molecule-surface system did not vary much from one surface site to another when the surface being considered was metallic. The reasoning was that the electrons on a metal surface spread out, i.e. they (at least the conduction electrons) are delocalised, and so the "electronic surface" is smoother than the "real one", as illustrated below.

A close-packed metal surface is shown from above on the left. When viewed side-on, right, you can see how the electrons (shown by red contours indicating constant density) spill over and fill in the bridge sites between the atoms.

Since it is the electrons that determine the bonding, and so therefore the bonding energy (i.e. the potential energy surface), then this must also be quite a smooth function of position across the surface, or so goes the argument. This seems to work reasonably for He interacting with a surface, but this is not really a chemical interaction. For molecules, where bonds break and re-form (or try to) this does not hold.

Here's an example of what I mean: the following two elbow potentials have been computed for hydrogen molecules (H₂) interacting with the (111) surface of Cu for different sites, but with the molecule in the same azimuthal orientation, i.e. to get from one to the other you just slide the molecule across the surface.

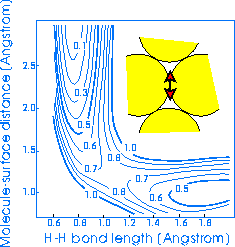
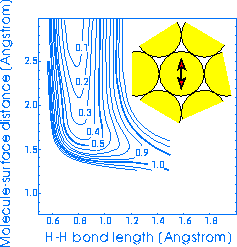
These potentials were calculated by Bjørk Hammer in Denmark, using a slab-supercell geometry to represent the surface. The energies on the countours are in eV.

Consider the left-hand one first; this is the PES for dissociation from the bridge site (the location of the molecular centre of mass) into the hollow site (where the two atoms end up). This is the most favoured dissociation route, and in fact the 'true' barrier height is lower than that obtained in this calculation. Note that the elbow bends round very smoothly.

Compare it now to the right-hand PES (for dissociation from on top of a surface atom with the H atoms going into the hollow-site again). Notice that the atop-hollow PES has a higher barrier, which occurs further from the surface and at greater bond-length (these two actually cancel out somewhat), and that it bends around much more sharply.

OK, so when the molecule comes down on different sites the PES looks different. But this is H₂ /Cu(111) !! This is a paradigm of activated dissociation dynamics which exhibits normal energy scaling !!

So in other words, even though the different sites have very different interaction PESs with different barrier heights, the dissociation still appears as if the surface is flat.

Why does it appear flat in the dissociation ?