|
Physical form of the model | ||
|
To apply a surface complexation model, a number of assumptions must be made about the character of the sediment. Lake sediment comprises a large number of particle types in addition to Fe and Mn oxyhydroxides. Each of these contributes to adsorption of ions from the pore-water. While much is known of the adsorption properties of pure minerals, there have been very few experimental studies on lake sediment in its undisturbed state. From simply theoretical consideration, however, it is clear that particle size is a key factor. Fe and Mn oxyhydroxides precipitated in situ within sediments have dimensions in the order of tens of nanometres. In contrast, the modal grain size of lake sediments is typically in the order of 10 micrometres. Even if these larger particles had adsorption properties identical to Fe and Mn oxyhydroxides, their size gives them a low specific surface area. A sediment in which 99% of the mass is in 10 Ám particles, and only 1% in 10 nm particles, the smaller particles will make up 91% of the surface area.
The model is thus based on the idea that migration of Fe and Mn oxyhydroxides should alter the concentration of available absorbing sites, and thereby alter the trace element dissolved concentration in the affected sediment. The basic physical model is illustrated to the right. | 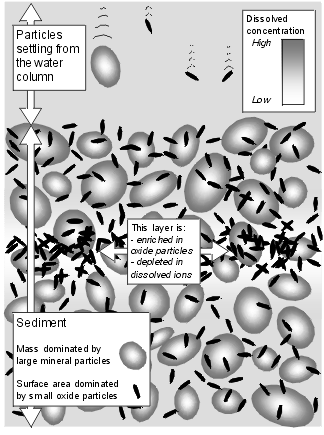 |
| Formulation of the model |
| Illustrated using Zn, the dissolved metal concentration is calculated using a surface complexation model: |
| 1 | 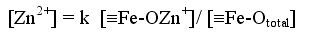 |
| Where [ ] indicates concentration, and the triple bar symbolises a particle surface | ||
| To apply the model it is necessary to know the relevant surface complexation coefficients. While these have been measured for a wide range of materials, there remains a problem in applying these directly to lake sediments. An alternative is to use the more widely measured distribution coefficient (Kd) as a data source. The distribution coefficient for Zn is defined as: |
| 2 | 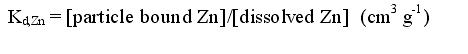 |
| It can be shown that for dilute cases (where few oxide adsorption sites are occupied by Zn ions), then Kd is proportional to k in the surface complexation model. |
| If it is assumed that the number of oxide adsorption sites is proportional to the sediment Fe concentration, then the value of Kd,Zn should vary through the sediment in proportion to the Fe concentration. The variation in Kd,Zn can be expressed in terms of deviation in the Fe concentration from a normal value (Fe0), and the normal Kd,Zn (Kd,Zn,0). Thus, Kd,Zn for any particular depth in the sediment profile, x, is given by equation 3. |
| 3 |  |
| This can be incorporated into a standard diffusion equation. The resulting partial differential equation can be solved explicitly to calculate the flux of trace metal resulting changes in adsorption site availability. |
| Results |
|
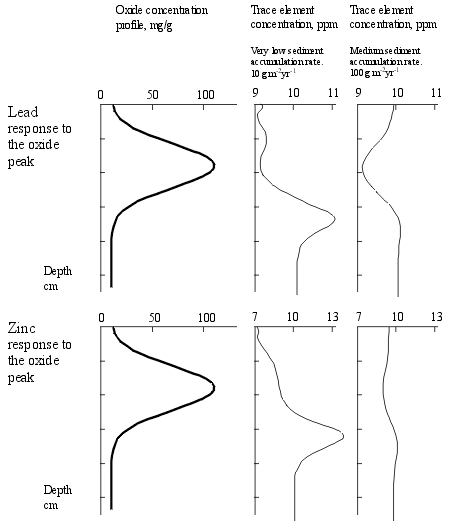
The sample runs shown here illustrate the response of Pb (relatively immobile) and Zn (relatively mobile) to an oxide peak, at two different sediment accumulation rates.
At the higher sediment accumulation rate the dominant effect is dilution (by the increase mass due to oxide influx). A very weak enhanced trace element concentration is seen beneath the oxide peak. At higher sediment accumulation rates the dilution effect remain, but the enhancement effect is even weaker. At the low accumulation rate, dilution is less important, and a distinct enhancement peak is visible. Note however, the weakness of this peak (1 ppm for Pb and 2 ppm for Zn). This would usually be lost in the noise of natural variability. |
 |