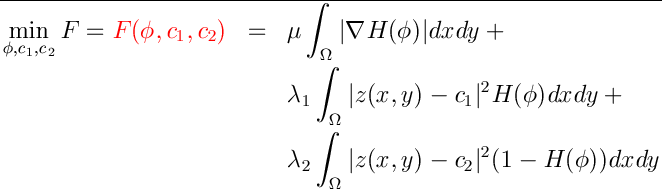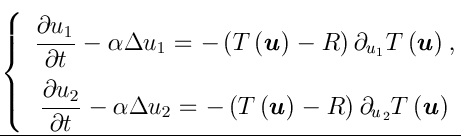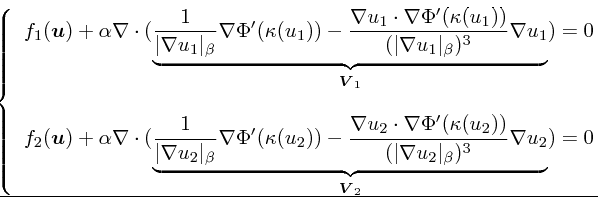-
 Iterative Methods for Solving Linear Systems and Related Problems
Iterative Methods for Solving Linear Systems and Related Problems
The numerical solution of partial differential equations and
integral equations in modelling various physical phenomena often requires
the solution of large systems (either sparse or dense) of linear algebraic
equations (either structured or unstructured).
The direct solution of these linear systems using Gaussian
elimination is prohibitively expensive in terms of both time and
storage, so iterative methods are used. These do not require storage of
the matrix but only the ability to perform matrix-vector
multiplications. An important area of research is to find efficient
iterative methods that require only a small number of matrix-vector
multiplications and a small amount of additional work to compute a good
approximate solution to the linear system.
Recent progress has been made in designing new sparse preconditioners
for conjugate gradient method and the minimal residual method for linear systems.
Current work deals with nonsymmetric problems.
This study involves Eigenvalues, Singular value decompositions, Operator splitting,
Wavelets, Various applications that include the fascinating subject of
image deblurring and denoising. (See
who cares about Ax=b ? and
also
Recent EPSRC grant)
References:
- 1999. Discrete wavelet transforms
accelerated sparse preconditioners for dense boundary element systems,
by Ke Chen, Electronic
Transactions on Numerical Analysis, V.8, pp. 138-153.
- 2000.
A new wavelet transform preconditioner for iterative solution
of
elastohydrodynamic lubrication problems.
by Judy Ford, Ke Chen and Laurence Scales,
International Journal of Computer Mathematics, vol.75,
pp.497-513.
- 2001.
Wavelet-based preconditioners for dense matrices
with non-smooth local features,
by Judy Ford and Ke Chen,
BIT
(J. Numerical Mathematics), 41, (2), 282-307.
- 2001.
An analysis of sparse approximate inverse
preconditioners for boundary integral equations,
by Ke Chen,
SIAM J. Matr. Anal. Appl., 22, (3), 1058-1078.
- 2001.
Wavelet-based preconditioning of dense linear systems ,
by J. M. Ford,
Ph.D thesis, University of Liverpool, UK.
- 2002.
On two variants of an algebraic wavelet preconditioner,
by Tony F. Chan and Ke Chen.,
SIAM Journal on Scientific Computing, 24, (1),
pp.260-283.
- 2005. A two-level sparse approximate inverse preconditioner for
unsymmetric matrices, by Ke Chen and Martyn D. Hughes,
IMA Journal of Numerical Analysis,
Vol 26 (1), pp.11-24.
[Download Paper (in pdf.gz) ]
-
 Numerical Solution of Boundary Integral Equations and Related Problems
Most scientific problems are formulated as partial differential equations which must be
solved numerically. Sometimes the solution can be expressed as a boundary integral
involving an unknown density function which can also be computed numerically by solving
an integral equation. Thanks to recently developed algorithms such as iterative linear
system solvers and the fast multipole method it is sometimes more efficient to solve the
integral equation. Recent work has dealt with the numerical solution of integral
equations and stable and efficient methods for evaluating the solution at various points
once the integral representation in known.
A typical problem is to compute the scattered acoustic field induced by an incident
wave passing a bounded obstacle.
The procedure for solving the problem is
to discretize the surface of the region using triangles, solve a boundary integral
equation to determine an integral expression for the solution, use this expression to
evaluate the discrete Helmholtz equation at the mesh points.
Fine resolution may require solution of large linear systems and often iterative
solvers.
Numerical Solution of Boundary Integral Equations and Related Problems
Most scientific problems are formulated as partial differential equations which must be
solved numerically. Sometimes the solution can be expressed as a boundary integral
involving an unknown density function which can also be computed numerically by solving
an integral equation. Thanks to recently developed algorithms such as iterative linear
system solvers and the fast multipole method it is sometimes more efficient to solve the
integral equation. Recent work has dealt with the numerical solution of integral
equations and stable and efficient methods for evaluating the solution at various points
once the integral representation in known.
A typical problem is to compute the scattered acoustic field induced by an incident
wave passing a bounded obstacle.
The procedure for solving the problem is
to discretize the surface of the region using triangles, solve a boundary integral
equation to determine an integral expression for the solution, use this expression to
evaluate the discrete Helmholtz equation at the mesh points.
Fine resolution may require solution of large linear systems and often iterative
solvers.
References:
- 1991. Conjugate gradient methods for the solution of
boundary integral equations on a piecewise smooth boundary,
by K. Chen,
Journal of Computational Physics, 97 (1), 127-143.
- 1993.
Numerical Analysis of Boundary Integral Solution of
the Helmholtz equation in domains with non-smooth
boundaries, by K. Chen and S. Amini,
IMA J. Numer. Anal., V13, 43-66, 1993.
- 2000.
A general DRBEM model for wave refraction and diffraction,
by S P Zhu, H W Liu and K Chen,
J. Engineering Analysis with Boundary Elements, vol.24, No.5,
pp.377-390.
- 2001.
Efficient preconditioners for
iterative solution of the boundary element equations for the
three dimensional Helmholtz equation,
by Ke Chen and Paul Harris,
Journal of Applied Numerical Mathematics, vol 36, pp.475-489.
- 2003.
On efficient preconditioners for iterative solution
of a Galerkin boundary element equation for the
three dimensional exterior Helmholtz problem,
by Paul Harris and Ke Chen,
Journal of Computational and Applied Mathematics,
vol. 141.
[Download Paper (in ps.gz)]
- 2005.
An implicit wavelet approximate inverse preconditioner, by Stuart
C. Hawkins and Ke Chen,
SIAM Journal on Scientific Computing,
Vol 27, Number 2, pp. 667-686.
[Download Paper (in ps.gz) ]
-
 Parallel Scientific Computing
The efficiency of numerical algorithms used to be measured by the number of operations
(additions, subtractions, multiplications, and divisions) required. Today, this may no
longer give a reasonable estimate of the relative performance of the methods. Data
locality and potential for parallelism (the ability to make effective use of multiple
processors simultaneously) are important properties of any numerical algorithm.
Parallel Scientific Computing
The efficiency of numerical algorithms used to be measured by the number of operations
(additions, subtractions, multiplications, and divisions) required. Today, this may no
longer give a reasonable estimate of the relative performance of the methods. Data
locality and potential for parallelism (the ability to make effective use of multiple
processors simultaneously) are important properties of any numerical algorithm.
Thus linear algebra algorithms may have to re-designed and implemented in such a way as
to minimize memory references and allow the greatest possible use of parallelism. This
is not about programming! It involves e.g. matrix partitions and function space
decompositions, and iterative solvers.
Recently with the birth of
MPI,
programming side becomes much easier so one can
concentrate more on developing new mathematical methods.
References:
- 1998.
Solutions of boundary element equations by a flexible
elimination process,
by C. H. Lai and K. Chen, Contemp. Math., 218, pp.311-317.
- 2000.
An efficient variant of Gauss-Jordan type algorithms for
direct and parallel solution of dense linear systems,
by Ke Chen and David Evans,
International Journal of Computer Mathematics, vol.76,
pp.387-410.
- 2001.
Flexible parallelization of fast wavelet
transforms, by
Judith Ford, Ke Chen and Neville J. Ford,
Journal of Parallel Algorithms and Applications,
pp.155 - 169, Vol 18 (4).
See also Numerical Analysis
Report 389,
Manchester Centre for Computational Mathematics.
- 2002.
Parallel algorithms of the Purcell method for
direct solution of linear systems,
by Ke Chen and C H Lai,
Journal of Parallel
Computing,
vol.28, no.9, pp.1275-1291.
[Download Paper (in ps.gz)]
-
 Adaptive Solution of Differential Equations
The usual technique in numerical solution of partial differential equations and
integral equations is to convert these equations into
matrix equations, by placing a mesh over the interested domain (2D or 3D) and
replacing the underlying unknown function by a piecewise polynomial. The mesh
must be fine enough to capture the `variation' of the unknown solution (function)
but the total number of mesh points must be restricted to obtain a computer
solution in a shorted time. Then the obvious challenge is to generate an intelligent
mesh which satisfy both criteria --- design an adaptive strategy.
This subject gives one the chance to understand
and research on a lot of mathematics.
Adaptive Solution of Differential Equations
The usual technique in numerical solution of partial differential equations and
integral equations is to convert these equations into
matrix equations, by placing a mesh over the interested domain (2D or 3D) and
replacing the underlying unknown function by a piecewise polynomial. The mesh
must be fine enough to capture the `variation' of the unknown solution (function)
but the total number of mesh points must be restricted to obtain a computer
solution in a shorted time. Then the obvious challenge is to generate an intelligent
mesh which satisfy both criteria --- design an adaptive strategy.
This subject gives one the chance to understand
and research on a lot of mathematics.
References:
- 1994.
Two Dimensional Adaptive Quadrilateral Mesh Generation,
by Ke Chen,
Comm. Numer. Meth. Engng., vol 10, 815-825, 1994.
(see abstract).
- 1994.
Error equidistribution and mesh adaptation,
by Ke Chen,
SIAM J. Sci. Comp., vol 15, 798-818.
- 2001. An adaptive mesh technique based on transforming the domains
and using tensor products for the dual reciprocity method,
by Kamal Shanarari and Ke Chen,
Proc. 3rd UK BIE conference, Brighton, UK.
- 2003.
A minimal distance constrained adaptive mesh algorithm with
application to the dual reciprocity method,
by Kamal Shanazari and Ke Chen,
Journal of Numerical Algorithms ,
vol.32, pp.275-286.
[Download Paper (in ps.gz) ]
-
 Novel mesoscale particle modelling methods for fluids
A robust technique of simulating complex fluid interaction
is the molecular simulation (MD) method. Unfortunately the method can
be very slow in getting the required simulation results because the
number of unknowns is imply too large (typically more than 1 million).
The recent emergence of mesoscale particle modelling methods offers
an interesting alternative and a fast solution to a large class of
complex problems. One such method is the dissipative particle dynamics
technique. The previous Liverpool has extended the method to solve
some challenging problems but many problems remain to be tackled both
in better analytical methods for simulation and in better numerical
schemes for solving the underlying time-dependent differential equations.
Novel mesoscale particle modelling methods for fluids
A robust technique of simulating complex fluid interaction
is the molecular simulation (MD) method. Unfortunately the method can
be very slow in getting the required simulation results because the
number of unknowns is imply too large (typically more than 1 million).
The recent emergence of mesoscale particle modelling methods offers
an interesting alternative and a fast solution to a large class of
complex problems. One such method is the dissipative particle dynamics
technique. The previous Liverpool has extended the method to solve
some challenging problems but many problems remain to be tackled both
in better analytical methods for simulation and in better numerical
schemes for solving the underlying time-dependent differential equations.
References:
- 1998.
Simulation of Particle Adsorption onto a Polymer Coated Surface
using the Dissipative Particle Dynamics Method,
by Jonathan Gibson, Ke Chen, Simon Chynoweth,
Journal of Colloid and Interface Science,
vol.206, 464-474.
- 1999.
Simulation of Colloidal-Polymer Systems using
Dissipative Particle Dynamics,
by Jonathan Gibson, Kai Zhang, Ke Chen,
Simon Chynoweth and Chuke Monke,
J. Molecular Simulation.
- 1999.
The equilibrium of a velocity-verlet type
algorithm for DPD with finite time steps,
by
Jonathan Gibson, Ke Chen, Simon Chynoweth,
International Journal of Modern Physics C, Vol. 10, No.1,
pp.241-261.
- 1999. Application and Analysis of Dissipative Particle Dynamics,
by Jonathan Gibson,
Ph.D thesis, University of Liverpool, UK.
-
 Bifurcation Methods for Nonlinear Power Equations
Kirchhoff's laws define voltage and current conservation equations
for two main variables (voltage magnitude and phase) of a power
transmission network (if you are a mathematician, read G. Strang's
1986 book of ``Applied Mathematics" to learn more).
Among other things,
power demand changes affect these variables that must be kept within
safety ranges. Computer simulation is a common practice here. However
for large networks, the currently available mathematical
methods are not adequate and there is an urgent need to develop fast
analytical as well as numerical techniques. One important on-line
control problem is to predict the maximal load margin allowable at a
particular location --- this margin is not allowed to bypass a
bifurcation point. The current Liverpool work has found satisfactory
methods for locating the fold index (load margin). Much work is needed
to locate the Hopf point in a fast way.
Bifurcation Methods for Nonlinear Power Equations
Kirchhoff's laws define voltage and current conservation equations
for two main variables (voltage magnitude and phase) of a power
transmission network (if you are a mathematician, read G. Strang's
1986 book of ``Applied Mathematics" to learn more).
Among other things,
power demand changes affect these variables that must be kept within
safety ranges. Computer simulation is a common practice here. However
for large networks, the currently available mathematical
methods are not adequate and there is an urgent need to develop fast
analytical as well as numerical techniques. One important on-line
control problem is to predict the maximal load margin allowable at a
particular location --- this margin is not allowed to bypass a
bifurcation point. The current Liverpool work has found satisfactory
methods for locating the fold index (load margin). Much work is needed
to locate the Hopf point in a fast way.
References:
- 2001.
"An analysis of Seydel's test function methods for
nonlinear power flow equations",
by Hussein A., Chen K., Wan H.B.
International Journal of Computer Mathematics,
Vol 78 (3), pp.451-470.
[Download Paper (in ps.gz)]
- 2002.
"On a Class of New and Practical Performance Indexes for Approximation
of Fold Bifurcation of Nonlinear Power Flow Equations",
by Chen K., Hussein A.,Wan H.B.
Journal of Computational and Applied Mathematics,
vol. 140, no. 1-2, pp. 119-141.
- 2002.
"On Adapting Test Function Methods for Fast Detection of Fold
Bifurcations in Power Systems" ,
by Hussein A., Chen K., Wan H.B.
International Journal of Bifurcation & Chaos,
vol. 12, no. 1, pp. 179-185.
- 2003.
"On Efficient Methods for Detecting Hopf Bifurcation
with Applications to Power System
Instability Prediction",
by Anwar Hussein and Ke Chen,
International Journal of Bifurcation & Chaos,
Vol. 13, No. 5,
pp.1247-1262 (2003).
[Download Abs
and Paper (in ps.gz)]
- 2003.
"A performance-index guided continuation method
for fast computation of saddle-point bifurcation in power systems".
by Ke Chen, Anwar Hussein, Martin Bradley and Haibin Wan,
IEEE Transactions on Power Systems
[Download Paper (in ps.gz)]
-
 Effective Variational Models and Efficient Numerical Methods for Solving Inverse Problems
Many applications of PDEs for modelling applied mathematical problems
are concerned with inverse formulation e.g. (i) given an observed image,
how to reconstruct the true image without noise and blur;
(ii) given a partial solution of a PDE,
how
to find its coefficients or boundary conditions;
(iii) given a (measured) scattered acoustic fields, find the scatterer (object).
The analytical tools
involve constrained minimisation techniques, Euler-Lagrange equations
and level set methods. Usually the less smooth (or differentiable) the
object functional is, the more useful are the results!
Such non-smoothness or non-differentiability translates into PDEs with highly
discontinuous or degenerate coefficients!
Efficient numerical solution techniques are in
urgent demand. Apart from developing new algorithms, our recent interests are centred on modelling image segmentation and image registration applications.
This subject is one modern example of large scale scientific
computing.
Effective Variational Models and Efficient Numerical Methods for Solving Inverse Problems
Many applications of PDEs for modelling applied mathematical problems
are concerned with inverse formulation e.g. (i) given an observed image,
how to reconstruct the true image without noise and blur;
(ii) given a partial solution of a PDE,
how
to find its coefficients or boundary conditions;
(iii) given a (measured) scattered acoustic fields, find the scatterer (object).
The analytical tools
involve constrained minimisation techniques, Euler-Lagrange equations
and level set methods. Usually the less smooth (or differentiable) the
object functional is, the more useful are the results!
Such non-smoothness or non-differentiability translates into PDEs with highly
discontinuous or degenerate coefficients!
Efficient numerical solution techniques are in
urgent demand. Apart from developing new algorithms, our recent interests are centred on modelling image segmentation and image registration applications.
This subject is one modern example of large scale scientific
computing.
In this field, nonlinearity plays a major role in preserving quality restoration (image
sharpness)
e.g. in the Poisson denoising model
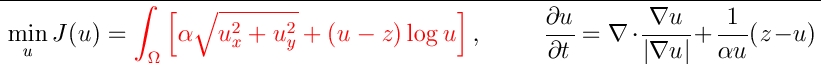 ,
,
the total variation term (of the optimization) or the denominator of the PDE makes up the main
nonlinearity, responsible for quality restoration as well as for
various numerical difficulties in developing fast algorthms (and in theoretical analysis).
- 2005. A nonlinear multigrid method for curvature
equations related to total variation minimization, by
Ke Chen and Xue-cheng Tai, UCLA
CAM report 05-26.
Journal of Scientific Computing,
Vol. 33 (2), pp.115-138, 2007.
- 2005. An improved and accelerated
nonlinear multigrid method for total-variation denoising,
by Joseph Savage and Ke Chen,
International Journal of Computer Mathematics,
Vol 82, (8), pp.1001-1015.
- 2006. On a nonlinear multigrid algorithm with primal relaxation
for the image total variation minimisation, by
Tony F. Chan and Ke Chen,
Numer. Algor.,,
Vol 41, pp.387-411.
[Download Paper (in pdf) ]
- 2006. An optimization based total variation image denoising,
by Tony F. Chan and Ke Chen,
SIAM J. Multiscale Modeling & Simulation ,
Vol 5(2), pp.615-645.
[Download Paper (in pdf) ]
- 2007.
"Iterative Methods for Solving the Dual Formulation
Arising from Image Restoration",
Electronic
Transactions on Numerical Analysis,
by Tony F. Chan, Ke Chen and J. L. Carter,
Vol.26, pp.299-311.
[Download Paper
(in pdf) ]
- 2008.
Fast multilevel algorithm for a minimization problem in impulse noise removal,
by Raymond H Chan and Ke Chen,
SIAM Journal on Scientific Computing ,
Volume 30 (3), pp.1474-1489.
[See Abstract]
and Paper (pdf in gz)]
- 2008.
Multigrid Method For A Modified Curvature Driven Diffusion Model
For Image Inpainting, by Carlos Brito-Loeza and Ke Chen,
Journal of
Computational Mathematics
Vol. 26, No.6 (2008), pp. 856-875.
[Download Paper (pdf in gz)]
- 2008.
Multigrid Method for the Chan-Vese Model in
Variational Segmentation,
Communications in Computational Physics (CiCP)
by Noor Badshah and Ke Chen
Vol.4 (2), pp.294-316.
[Download
Abstract and pdf]
- 2009.
A Robust Affine Image Registration Method,
by Noppadol Chumchob and Ke Chen,
Vol 6 (3), pp.311-334, 2009.
International Journal of
Numerical Analysis and Modeling
[Download PDF]
- 2009.
On Two Multigrid Algorithms for Modelling Variational Multiphase
Image Segmentation, by Noor Badshah and Ke Chen
IEEE Transactions on Image Processing,
Vol. 18(5), pp.1097-1106, 2009.
- 2010.
SIAM Journal on Imaging Sciences , ``Multigrid Algorithm for High
Order Denoising'', by Carlos Brito and Ke Chen, Vol 3 (3), pp.363-389
[PDF]
- 2010.
IEEE Transactions on Image Processing
, ``On high order denoising
models and fast algorithms for vector-valued images'',
by Carlos Brito and Ke Chen, Vol 19 (6), pp.1518-1527
[PDF]
- 2010.
SIAM Journal on Scientific Computing ,
``A Multilevel Algorithm for Simultaneously Denoising and Deblurring Images'',
by Raymond H Chan and Ke Chen, Volume 32, Issue 2, pp. 1043-1063
[PDF]
- 2011.
SIAM Journal on
Multiscale Modeling & Simulation ,
``A fourth order variational image registration model and
its fast multigrid algorithm",
by Noppadol Chumchob, Ke Chen and Carlos Brito,
Vol 9 (1), pp.89-128.
[PDF]
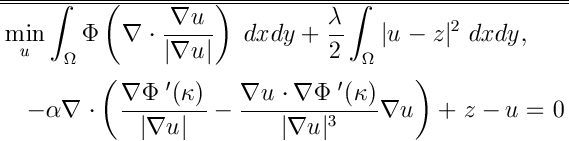 and
and
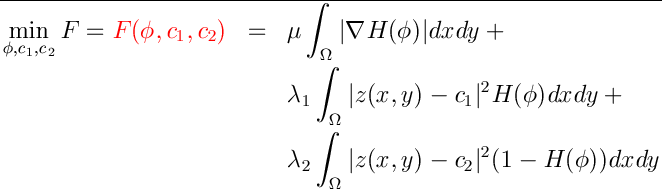
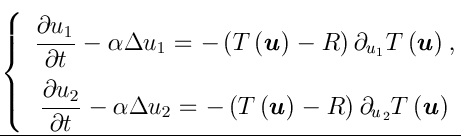
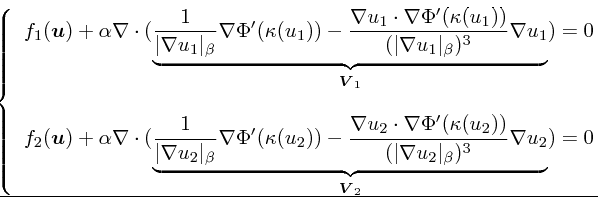
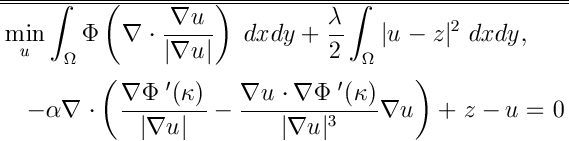 and
and